Page 84 - 《应用声学》2020年第2期

242 2020 年 3 月

动参数估计，由于接收声场具有足够的信噪比，因 非线性最小二乘法进行参数估计的准确性。此外，
此可直接利用峰值检测法提取出瞬时频率随时间 将由真实运动参数计算得到的瞬时频率绘制为图 8
的变化曲线，而后通过非线性最小二乘法估计运动 中黑色实线，对比黑色实线与蓝色虚线可以发现，瞬
参数。瞬时频率的提取曲线与运动参数估计结果分 时频率提取的误差是造成运动参数估计误差的主
别由图 8 和表 1 给出，四个参数估计误差均在 6%之 要因素。在信噪比较高的情况下，可结合 PCT [13] 、
内，准确度较高。 Doppler-CT [14] 等时频分析方法提高时频分析的聚
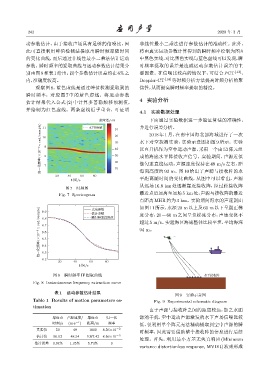
观察图 8，蓝色虚线是通过峰值检测提取到的 焦性，从而提高瞬时频率提取的精度。
瞬时频率，对应图 7 中的蓝色虚线。将运动参数
4 实验分析
估计结果代入公式 (2) 中计算多普勒频移预测值，
并绘制为红色虚线。两条虚线近乎重合，可证明
4.1 实验数据处理
下面通过实验数据进一步验证算法的准确性，
ᑟ᧚៨/dB 并进行误差分析。
ॆʷӑᮠဋ(T10 -3 p rad/sample) 10 9 8 -20 水下对空探测实验，实验示意图如图 9 所示。实验
ඵʾઉ࠱ฉ
11
-10
2018 年 1 月，在南中国海北部海域进行了一次
-30
以直升机作为空中运动声源，采用一个由53阵元组
-40
成的海底水平阵接收声信号。实验期间，声源近似
-50
-60
7
海面高度约 93 m。图 10 给出了声源与接收阵的水
20 40 60 80 -70 做匀速直线运动，声源速度保持在 49 m/s 左右，距
௑ᫎ/s 平距离随时间的变化曲线，从图中可以看出，声源
从远场 16.8 km 处逐渐靠近接收阵，经过距接收阵
图 7 时频图
最近点后远离至远场5 km处，声源与接收阵的最近
Fig. 7 Spectrogram
点距离 MHR约为3 km。实验期间海水的声速剖面
如图 11 所示，水深 20 m 以上及 60 m 以下呈弱正梯
ॆʷӑᮠဋ(T10 -3 p rad/sample) 8.7 超过5 m/s。实验海区海底整体比较平坦，平均海深
ᄾࠄԠ஝
8.9
ͥᝠԠ஝
度分布，20 ∼ 60 m 之间呈负梯度分布，声速变化不
ᅯ௑ᮠဋଢԩϙ
8.8
94 m。
8.6
8.5
8.4
8.3
8.2
20 40 60 80
௑ᫎ/s

图 8 瞬时频率 IF 提取曲线 ඵࣱଌஆ᫼
Fig. 8 Instantaneous frequency extraction curve
表 1 运动参数估计结果
图 9 实验示意图
Table 1 Results of motion parameters es- Fig. 9 Experimental schematic diagram
timation
由于声源与接收阵之间的距离较远，加之水面
最近点 声源速度/ 最近点 归一化 源的干扰，空中运动声源激发的水下声场信噪比较
时刻/s (m·s −1 ) 距离/m 频率 低，仅利用单个阵元无法精确提取到空中声源的瞬
真实值 50 49 1000 8.56×10 −3
时频率，因此需要借助整个接收阵的信息进行后续
估计值 50.02 48.34 1057.42 8.56×10 −3
处理。首先，利用最小方差无失真响应 (Minimum
估计误差 0.04% 1.35% 5.74% 0
variance distortionless response, MVDR)波束形成