Page 86 - 《应用声学》2020年第2期

244 2020 年 3 月

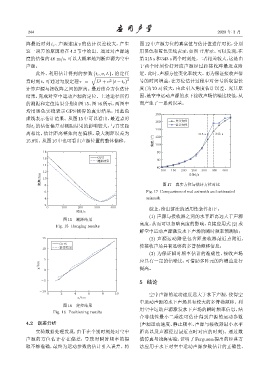
阵最近时刻 t c 、声源速度 v 的估计误差较大，产生 图 12中声源方位的真实值与估计值进行对比，分别
这一误差的原因将在 4.2 节中给出。通过对声源速 用黑色和蓝色实线表示，如图17所示。可以发现，在
度的估值约 46 m/s，可以大概率地判断声源为空中 第315 s和343 s两个时刻处，二者相差较大，这是由
声源。 于两个时刻恰好对应声源经过距接收阵最近点附
此外，利用估计得到的参数 {t c , v, L}，给定任 近。此时，声源方位变化率较大。而为保证接收声信
√
2
2
意时刻 t，可通过勾股定理 r = L + v (t − t c ) 2 号的时间增益，在方位估计过程中对信号所取窗长
计算声源与接收阵之间的距离。最后结合方位估计 度 (为 70 s) 较大，由此引入角度估计误差。究其原
结果，完成对空中运动声源的定位。上述途径所得 因，是空中运动声源的水下接收声场信噪比较低，从
的测距和定位结果分别如图 15、图 16 所示，两图中 而产生了一系列误差。
均用黑色实线表示 GPS 测得的真实结果，用蓝色
180
虚线表示估计结果。从图 15中可以看出，最近点时
160 ᄾࠄவͯ
刻 t c 的估值偏差对测距结果的影响较大，与真实距 ͥᝠவͯ
140
离相比，估计距离整体向左偏移，最大测距误差为 120 315 s 343 s
ᝈए/(°) 100
15.8%。从图16中也可看出声源位置的整体偏移。

18 80
16 GPS 60
฾ᡰፇ౧
14
40
100 150 200 250 300 350 400
12 ௑ᫎ/s
ᡰሏ/km 10 图 17 真实方位与估计方位对比
8
6 Fig. 17 Comparison of real azimuth and estimated
4 azimuth
2
0 100 200 300 400 综上，给出算法的适用性条件如下：
௑ᫎ/s
(1) 声源与接收器之间的水平距离远大于声源
图 15 测距结果
高度，从而可以忽略高度的影响，直接应用式 (2) 求
Fig. 15 Ranging results
解空中运动声源激发水下声场的瞬时频率预测值；

15 (2) 声源运动路径包含距接收器最近点附近，
GPS 使接收声场具有足够的多普勒频移信息；
10 ࠀͯፇ౧
(3) 为保证瞬时频率估计的准确性，接收声场
5 应具有一定的信噪比，可借助多阵元的阵增益进行
y/km
0 提高。

-5 5 结论

-10
0 2 4 6 8 10 空中声源的运动速度远大于水下声源，使得空
x/km
中运动声源的水下声场具有较大的多普勒频移。利
图 16 定位结果
用空中运动声源激发水下声场的瞬时频率信息，结
Fig. 16 Positioning results
合非线性最小二乘法可估计得到声源的运动参数
4.2 误差分析 (声源运动速度、静止频率、声源与接收器最小水平
实验数据处理发现，由于在个别时刻处对空中 距离以及声源经过最近点时对应的时刻)。通过数
声源的方位估计存在偏差，导致对瞬时频率的提 值仿真与浅海实验，证明了 Ferguson提出的经典方
取不够准确，最终为运动参数的估计引入误差。将 法应用于水下对空中运动声源参数估计的正确性。